回路計算ができないと結局自分が困る
皆さんは回路計算について難しいと感じていますか?
アイエルは計算するのはともかくとてもメンドクサイと思っています。
LTSPICEをはじめ最近の回路シミュレーションは優秀なので、直流・交流を問わず、回路規模も比較的複雑なものでの過渡解析もある程度の時間を掛ければ結果を教えてくれます。
しかし、入力した回路に対しての出力結果が自分の予想と異なることも多々あると思います。
この場合は、
- 設計は正しかったが、入力した回路にミスがあった。
- 入力した回路は正しいが、設計者側に勘違いがあり結果が異なる。
- 入力した回路は正しいが、理想部品だったため結果が異なる。
等が考えられます。
①については、回路を確認する必要がありますが最終的には差異がありますのでがんばれば発見できるかもしれません。
②と③の場合はどこに原因があるのか突き止めないと永遠に終わりません。
予想と違う場所を特定するためには最低限の回路計算ができないと設計の根拠が「シミュレーターが正しかったから!!」と言い張るしか無く、更にもし別のシミュレーターで違う結果が発生した場合は2つのシミュレーターの差異が説明できないと困ることになります。
なので、基本的な回路計算はできる必要があります。
ここでは最低限「オームの法則」は知っているものとして話を進めて行きます。
(オームの法則:電圧=電流×抵抗)
抵抗直列回路とは?
抵抗直列回路はその名の通り、電源に2つ以上の抵抗を直列に接続した回路です。
図にするとこんな感じ。
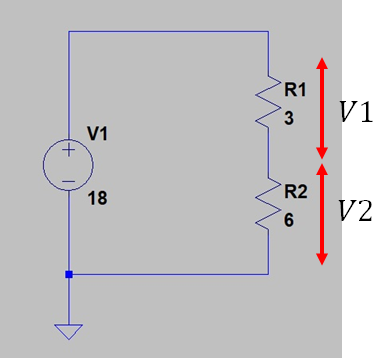
図1 直列回路1
で、R1とR2にかかっている電圧の計算は、電流がわからなくても求めることができます。R1にかかる電圧をV1、 R2にかかる電圧をV2として計算すると、
で計算していると思います。
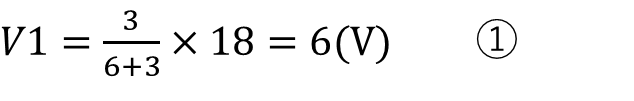
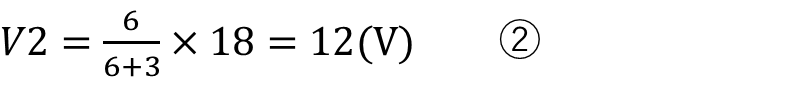
3素子の場合でも同様に
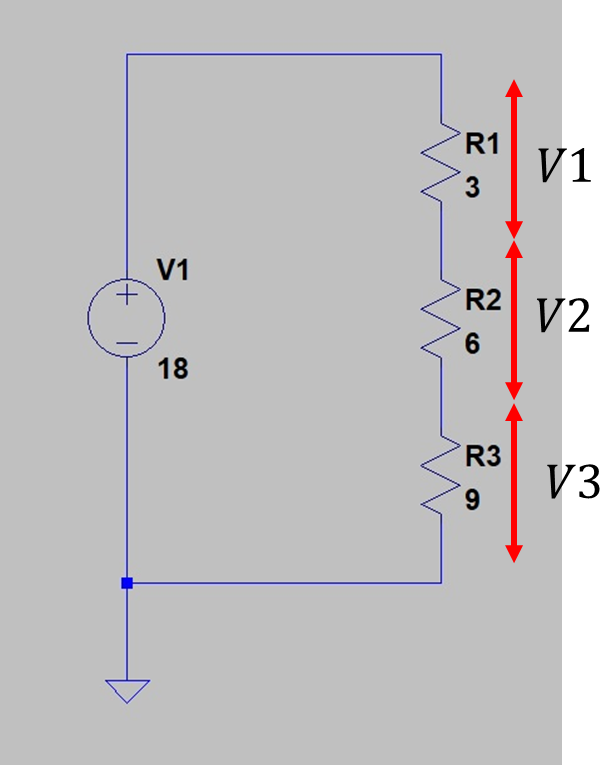
図2 直列回路2
で計算していると思います。
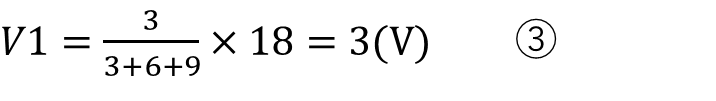
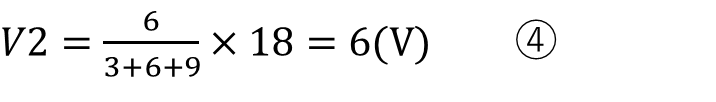
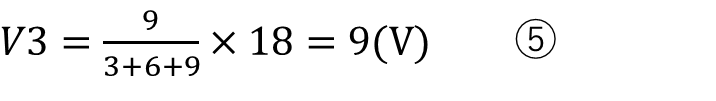
これだけだけでは計算できないパターンもある
でも、次の場合は先程のパターンでは計算できません。
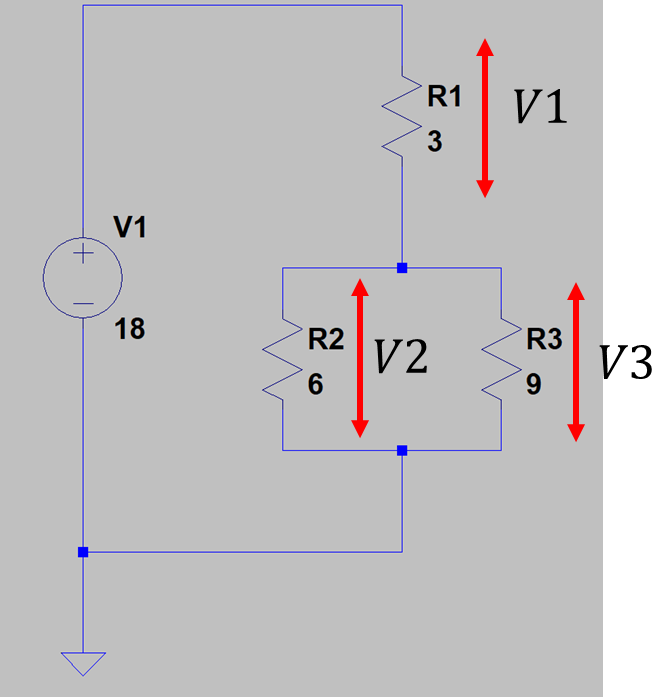
図3 直列並列回路
では何故図3は図1と図2と同じように計算がでいないのか?
回路図的にはR2とR3が並列になっています。この2つの抵抗に接続されています。
たったこれだけの違いですが、先程までの計算方法が通用しません。
何故計算できないのか
では何故このままでは計算ができないのでしょうか。
計算問題で引っかかる方は、公式を暗記しているが、内容が理解できていないので応用できない場合が多いと思います。アイエルもそうでしたので・・・
なのでメカニズムを知ることで理解いただければと思います。
計算を細かくすると・・・
図2の回路にある電源及び抵抗に流れる電圧と電流を下記のように記載します。電圧については先程までは素子の電圧差を表すために両矢印にしていましたが、今回は電流の方向性があるので電圧にも方向性を持たせるために方矢印にしています。
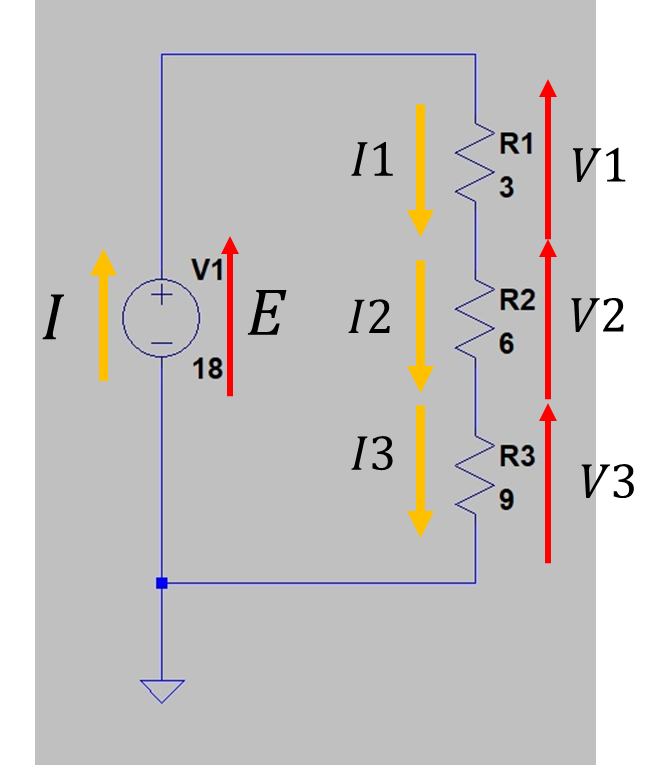
図4 図2に電圧及び電流を記載
オームの法則はV=R×Iになります。
各抵抗の電圧と電流の関係は
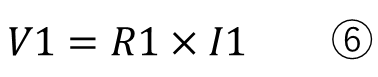
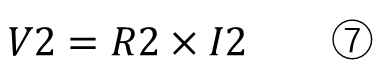
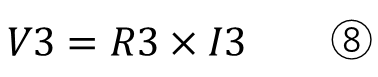
そしてここからが重要になります。
各素子と電源の関係性の式が必要になります。
電源の電圧と各素子の電圧の関係性の式は
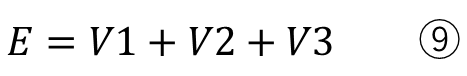
電源の電流と各素子の電流の関係性の式は
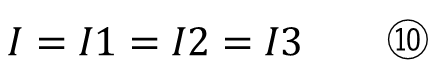
になります。
ここで⑨に⑥~⑧を代入すると
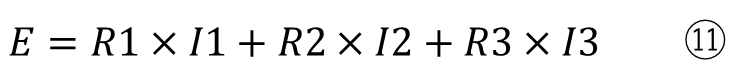
になります。
更に⑩を⑪に代入すると
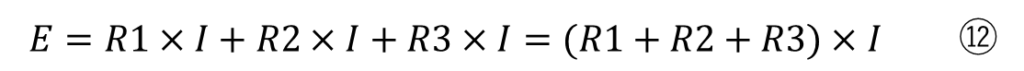
になります。
この式で電源の電圧に対して電流と抵抗の関係がわかるようになりました。
求めたい電圧をV1としたとき、⑥に⑩を代入すると
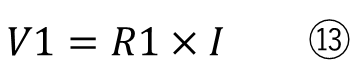
となります。そしてこの⑬を⑫で割ると
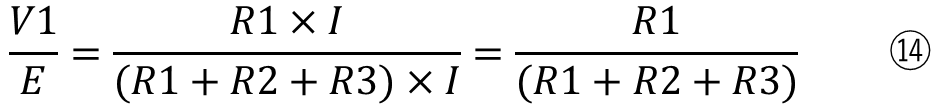
が導出できます。この式は電源電圧と素子の電圧は抵抗の大きさに比例する事を示しています。
この式は
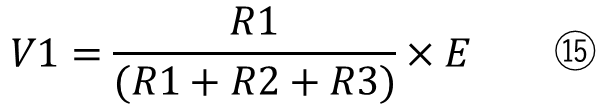
と変形できます。そして⑮に数値を入れたものが①で値を計算することができるのです。
以上が抵抗直列回路の計算になります。
抵抗直列回路で一番重要なこと
抵抗直列回路の計算で一番重要なことはたった1つです。
それは・・・
各素子の電圧が抵抗と比例関係にあるのは前提として各素子の電流が同一だからです。
ここの部分がとても大事でこの前提が崩れるとこの方法では計算ができなくなります。
まとめ
今回のまとめです。
- 抵抗値に掛かる電圧の総和と電源電圧の値は等しい
- 抵抗直列回路は抵抗値と抵抗に掛かる電圧は比例関係である
- この計算ができるのは直流抵抗回路の各抵抗値の電流が等しいからであり、並列だと各素子の電流が同じにならないので成立しない
最後に
「何当たり前な事と言っとるんや!」とお叱りを受けるかも知れませんが、実際はこの考え方はとても重要だとアイエルは考えいます。
公式を覚え何回も計算問題をしていると、パターン化して計算できるようになります。しかし、後輩に教えると考えたとき「どのようにして計算するのか」は教えることはできても「何故そうなるのか」を教えることは意外と難しいです。
アイエルは当たり前のことは当たり前として、それをどのように伝えるのかは相当難しいと思いこのようなブログを書いています。
計算をするスピードは、コンピューターを使う時代では個人の計算の時間差は意味が無くなってきています。しかし、式を立てるのはまだまだ人間が行う領域です。そして最終的にその計算結果の確認とそれを使った製品を世に出すのも人間の判断になります。



