抵抗とインピーダンスで混乱した経験
会社で技術的な話をしている場合、素子に関して色々な言い方をする人がいます。ある人は抵抗と言ったり、別の人はインピーダンスと言ったりして頭の中が混乱した経験はありますか?
アイエルは色々な人と話をしているうちに何を言っているのかがわからない経験をしたことがあります。
若手の時はネットが普及してないので調べるの大変な時代、そしてそれを理解するのがもっと大変な時代(初心者に厳しい挿絵も無く難解な式が記述しているだけ)だったのでちょっとしたニュアンスでも混乱しました。
抵抗?インピーダンス?どのように考えればよいのか
抵抗と言ったりインピーダンスと言ったり人によって色々と変わるのですがぶっちゃけちゃうと抵抗はインピーダンスと置き換えても問題ありません。
しかし、インピーダンスを抵抗と置き換えるのは注意が必要です。
今回はその辺りの解説をしたいと思います。
最初に学ぶのは抵抗
アイエルが小学生の頃、学校の理科(当時は理科と社会科がありました)で乾電池に豆球(当時は懐中電灯で使うものですが、今もあるのかな?)を接続して電圧と電流の関係を学ぶ実験がありました。
豆球を2個直列にすると1個の時より暗くなるのは当時はよくわかりませんでした。
当時学んだのは
- 豆球を2個直列にすると1個より暗く光る
- 豆球を2個並列にすると1個と明るさは同じだが電流が多くなり電池が早く寿命を迎える
だったと思います。
授業の実験では豆球の明るさは実感できましたが、時間がかかるので電池がなくなるまでややることはありませんでした。このときのアイエルは「そ~なんやぁ~」程度だっと思います。
で、中学で抵抗なるものが出てきて
- 電池(直流電圧源)と電流と抵抗の関係(オームの法則)
- 抵抗の直列や並列の計算
を学んだと思います。そして小学生で学んだ豆球が抵抗であったことを知ります。
なので、ここまではインピーダンスが出てこなかったと思います。
高校でインピーダンスが登場
高校では物理でインピーダンスが登場します。そしてインピーダンスとセットで覚えるものが色々出てきます。
- 交流電源
- コンデンサ
- コイル
- アドミタンス
- その他
ここでわからなくなる人も多いと思います。そして運動方程式も加わり挫折する人が多いと思います。
大学だと電気系の専攻では電磁気学を学ぶので更に挫折します・・・。
で、インピーダンスのお話の前に・・・
これまでの内容を整理すると
- 直流電源では抵抗しかなかった
- 正弦波を出力する交流電源が登場し、素子も抵抗の他にコンデンサとコイルが登場した
- 抵抗をインピーダンスと置き換えてても良いが逆は注意が必要
になります。
ここで重要なのが②で、交流電源が登場しからコンデンサとコイルを学ぶ必要がでてきたのです。
直流電源とコンデンサの関係
コンデンサは2枚の金属平行板に絶縁物を入れる構成です。この構成は電荷を溜める性質を持ってます。交流電圧は常に電圧が変動しますので、それに合わせてコンデンサの電荷も変動し電流が流れます。しかし、直流電圧は電圧が変動しません。コンデンサには絶縁物を挟んでいるのでコンデンサは直流電圧に対しては電流を流しません。コンデンサは直流電源対して解放(オープン)として扱います。
直流とコイルの関係
コイルは電線をらせん状に巻く構成になっています。この構成は電流を維持しようとする性質を持ちます。更にこの電流を維持しようとするために、変化した電流を打ち消そうとするような逆起電力が発生します。コンデンサと違いコイルはこの電流を維持しようとするイメージがしにくいので、アイエルはこれを理解するのに苦しみました(今も結構苦しんでいますが)。コイルは変化する電流に対してそれを妨げるような動きをするのですが、直流電圧の場合は電圧の変化が無いので電流の変化もありません。そして元々は電線を巻いただけですので、コイルは直流に対してはただの同線でしかありません。コイルの両端に直流電圧源を接続すると電圧源をショートさせる事と同じになります(危険ですのでやめてください)。コイルは直流電源に対して短絡(ショート)として扱います。
交流電源と抵抗、コンデンサ及びコイルの関係性
既知の人が大半だと思いますが、抵抗と同じようにコンデンサとコイルにも性能を表す単位があります。
交流電源と抵抗の関係性
交流電源と抵抗の関係はそのまま直流電圧源と抵抗の関係性に置き換えて問題ありません。
もうほとんど販売しておりませんが白熱電球は抵抗そのもので、直流電圧源での豆球と意味合いは全く同じです。違うのは直流電圧に接続されている豆球は常時点灯しているのに対して、交流電源に接続されている白熱灯は1秒間に50または60回点滅していることです。
この1秒間に繰り返す単位はHz(ヘルツ)として規定されています。日本では交流電源は50Hzまたは60Hzと地域によって決まっています。
この白熱灯の点滅は、人間の目には速すぎて常時点灯しているように感じます。
余談になりますが、昔の性能の低いドライブレコーダーではフレームレートが60fpsの(フレームパーセカント:1秒間で画像を取り込むことができる回数)でした。この録画性能が信号機の60Hzと同じなので、タイミングが悪いと常に消灯している動画もありました。最近では信号のLED化で点滅しなくなったのとドライブレコーダーのフレームレートが上がり常に消灯する動画になることは殆ど無くなりました。
交流電源とコンデンサの関係性
コンデンサの容量(キャパシタンス):F(ファラッド) 式の変数にはCを使うため「C値」と呼ぶこともあります。
交流で使うにはそのままで使用することはできません。
交流電源とコイルの関係性
コイルの誘電率(インダクタンス):H(ヘンリー) 式の記号にはLをを使うため「L値」と呼ぶこともあります。
こちらも交流で使うにはそのまま使用することはできません。
コンデンサとコイルを抵抗のように扱うには?
抵抗(上記に合わせると抵抗率)の単位であるΩ(オーム)とは違うのでそのままでは扱う事ができません。
本来であればこの抵抗、コンデンサ及びコイルを含めた式は微分方程式を解く必要があります。
しかし、以下の条件を満たしていれば比較的簡単に求めることができます。
- 電源投入時から十分な時間が経っていること
- 交流の周波数が1種類であること
- 抵抗、コイル、コンデンサのみで構成されていること
①については電源を投入すると各素子の電圧が計算値になるまでに一定時間がかかります。これは微分方程式に出てくる過渡現象を理解する必要があります。この過渡現象は十分に時間を置けば0に収束する場合が多いです。
②については違う周波数の電源があると正弦波と異なる波形になります。フーリエ解析等を勉強する必要がありますが単純な正弦波の電圧が理解できていないと厳しいです。
③についてはオペアンプ等の増幅回路が入った場合、①で述べたような時間を置けば0に収束しないことがあります。これも微分方程式や過渡現象を理解する必要があります。
交流電源を直流電源のように扱うための学問
昔の人は考えました。折角オームの法則があるのだから交流もオームの法則のように扱う事ができないかと。
そして創り出された学問が「交流理論」です。高校で物理を選択していれば学習していると思います。
オームの法則は電圧と電流と抵抗の関係性を表す内容で式は

抵抗成分はRの部分で単位はΩ(オーム)でした。
この直流電源で表した式に交流を当てはめるようなイメージになります。
交流で表すと

になります。このVやIの上に点がついているのが交流の証です。
直流では電圧は正極と負極が決まっており、正極側から電流が発生し負極側に流れますので、電圧も電流も正か負かの2方向しかありません。しかし、交流の場合は正弦波になります。正弦波は半周期毎に正側と負側が反転しますので、決めることはできません。
例えば交流100V電源を式にするとこんな感じになります。
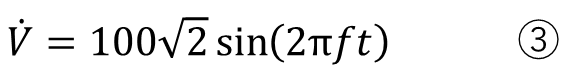
f:周波数(Hz) 日本の電力会社だと50or60Hz
t:時間(s)
時間tによって電圧の値は変化します。ここが直流電圧源との最大の違いです。
√2や2πとかはあまり気にしないでください。このあたりを解説するとそれだけで1つの話が出来上がってしますので。書きながら脱線しているなぁとは思っています(汗)。
抵抗(レジスタンス)の場合
で、抵抗の場合は交流でも直流でも同じ計算になります。
例えば2Ωの抵抗に50Aの電流を流した場合は、
直流だと
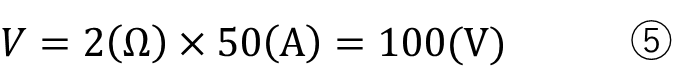
交流だと
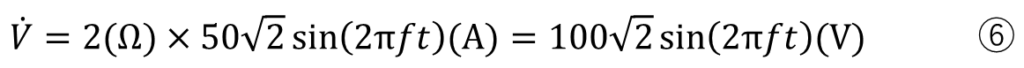
になります。
しかし、いちいち√2とsinを入れるのは大変なのでこの部分をACとして略します。
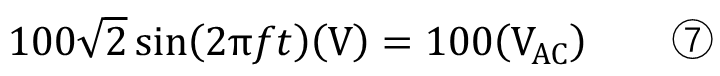
直流でも交流でも変わりません。
コンデンサの場合
最初に抵抗に相当するものを記載します。
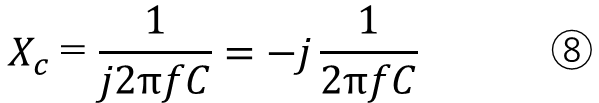
XC:容量性リアクタンス 単位は「Ω」(オーム)
C:静電容量(キャパシタンス) 単位は「F」(ファラッド)
f:周波数 単位は「Hz」(ヘルツ)
このXcは静電容量をそのまま使うのではなく周波数一緒に使います。違和感があるかも知れませんが単位はΩです。変数は分母にあるので、キャパシタンスと周波数が大きいほどこの値は小さくなります。
直流の場合は周波数を0としたいのですが、0で割ることができないので極小値で割るとXC無限大になりますので解放(オープン)となります。
jも記載されていますが、これは「虚数」を表します。数学では「i」を用いますが、電気ではiは電流で用いられる事が多いので区別をするために「j」を用います。
コイルの場合
こちらも最初に抵抗に相当するものを記載します。
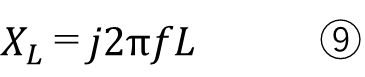
XL:誘電性リアクタンス 単位は「Ω」(オーム)
L:誘電容量(インダクタンス) 単位は「H」(ヘンリー)
f:周波数 単位は「Hz」(ヘルツ)
このXLは誘電容量をそのまま使うのではなく周波数一緒に使います。こちらも単位はΩです。変数は分子にあるので、インダクタンスと周波数が大きいほどこの値は大きくなります。
直流の場合は周波数を0にすると、XLは0になりますので短絡(ショート)となります。
こちらも虚数が入っています。
コンデンサとコイルは虚数があるのは同じですが、コンデンサはマイナスでコイルはプラスになっているので注意が必要です。
抵抗とコンデンサとコイルのΩの計算
先程の内容をまとめると
- 交流でも直流のように計算することができる
- コンデンサはキャパシタンスをそのまま抵抗のように扱う事ができない
- コンデンサはキャパシタンスと周波数を使って容量性リアクタンスを計算することで抵抗のように扱う事ができる
- コイルはインダクタンスをそのまま抵抗のように扱う事ができない
- コイルはインダクタンスと周波数を使って誘導性リアクタンスを計算することで抵抗のように扱う事ができる
- 抵抗は実数になっているがリアクタンスは容量性、誘導性の両方とも虚数が入っている
- 虚数部は誘導性はプラスで容量性はマイナスになっている
交流における抵抗のようなものは抵抗の他にコンデンサとコイルも入ってきます。
そこで実数部分をレジスタンスとして虚数部分をリアクタンスと分けています。
面白いのはこの実数部と虚数部はそれぞれ抵抗のように扱う事ができます。
例えばLCR直列回路の場合回路図は以下になります。
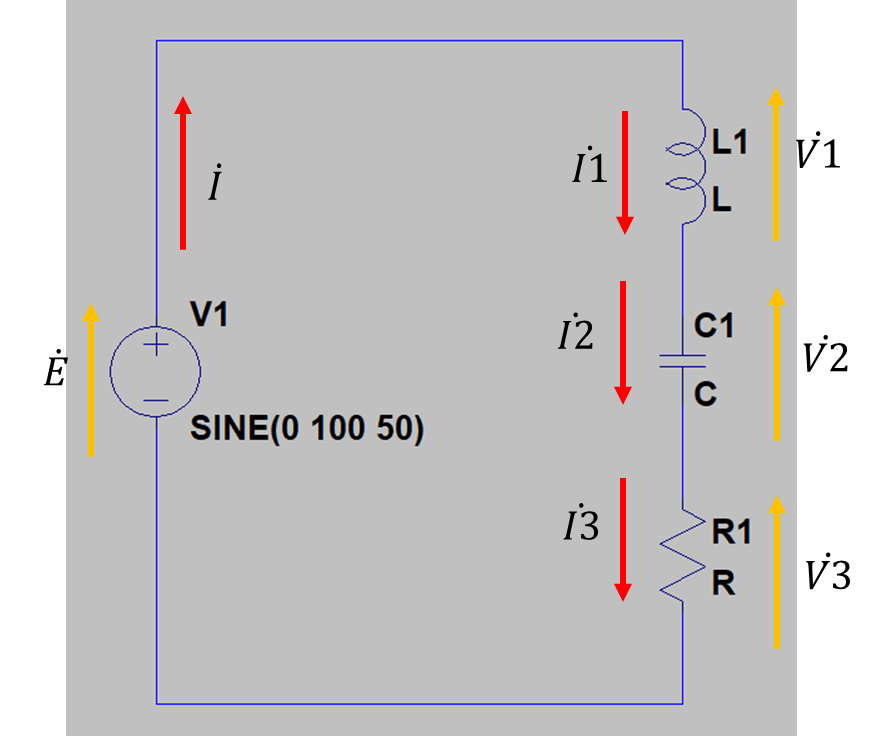
図1 交流直列回路
交流なのに矢印があるのはなんでや?と思う人があるかもしれません。交流の場合は式⑦のようにsinが入っています。このsinの方向に応じて正負を決めています。
基本的にsinが0→1→0→ー1→0と一周する方向を正側としています。交流の場合は色々な位相が入りますので固定されている電源を基準にしていると思って頂ければとと思います。
で、交流理論はコイルやコンデンサであってもオームの法則の様に扱う事ができます。
式⑧、⑨でコイルやコンデンサを抵抗のように扱うと
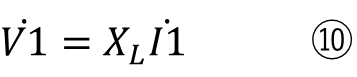
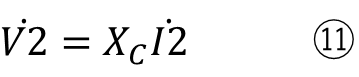
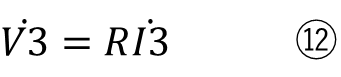
抵抗及びインダクタンスの単位は共にΩです。
交流なので電圧と電流にベクトルを表す「点」を付けています。
求め方そのものも変わりませんので、
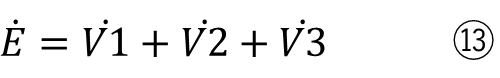
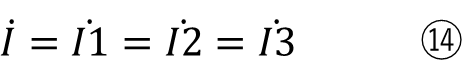
になります。
式⑩~⑭を整理すると
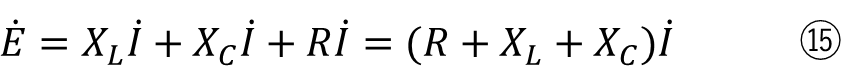
になります。
ここでインダクタンス部分に式⑧と⑨を代入すると
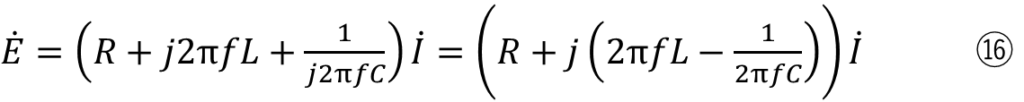
になります。
虚数が入っているので計算をするのが大変かもしれませんが、この虚数部があることで電圧と電流の間には大きさの変化だけでなく直流にはない位相差も表すことができます。
これより先は交流についてのより深い知識が必要になります。(ガウス平面とか極座標とか・・・)
各素子の電流は位相を含めて全く同じになりますが、電圧は各素子で大きさも位相も異なります。更にコイルとコンデンサのインダクタンスは周波数によっても値が変化するので注意が必要です。
そしてようやくインピーダンスの説明
先程の式⑮と⑯をオームの法則のように見立てると以下になります
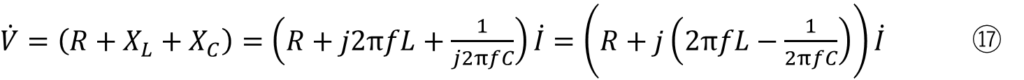
Eは電源でしたのでVに置き換えています。
VとIについては上に「点」がついていますが、内容は全く同じです。交流か直流かの違いです。
ここでこの抵抗(インピーダンス)とインダクタンスの部分は実数部と虚数部に分かれていますが、これを別々に書くのが大変なのであらかじめインピーダンスとインダクタンスをまとめて直流回路の「抵抗」に相当するものを定義した方が記載が楽になります。
この直流回路の抵抗に相当する部分を交流回路ではインピーダンスと定義されています。
比較するとこんな感じになります。
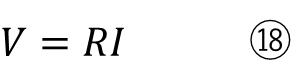
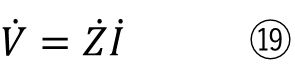
⑱が直流で⑲が交流になります。
直流の場合は抵抗は大きさを表すだけなので、電流の方向で電圧の方向が決まります。しかし交流の場合は、インピーダンスには大きさだけでなく方向もあります。大きさが同じインピーダンスでも方向が変わると電圧の方向も変わりますので注意が必要です。
これもガウス平面等色々な知識が必要になります。
大きさと位相差は以下になります。
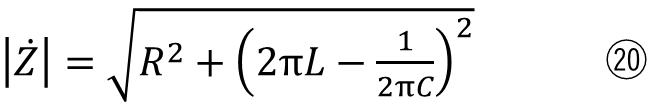
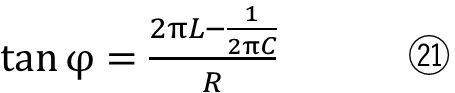
この⑳と㉑が元々の交流電流にかかることで、電圧の大きさと位相が変化します。
レジスタンス、容量性インダクタンス及び誘導性インダクタンスをまとめてインピーダンスとした場合以下の回路図になります。
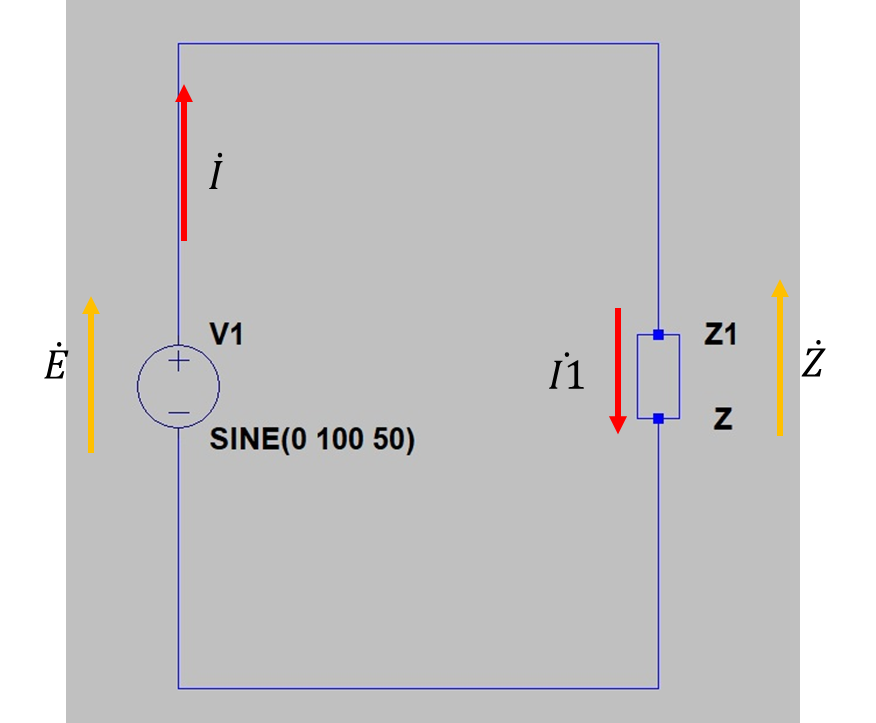
図2 交流回路2
図だけでは直列と変わらないのですが、電圧と電流に位相差が発生する場合があるのでここだけは注意が必要です。
まとめ
まとめると以下になります。
- インピーダンスはレジスタンスとインダクタンスに分類される。
- インダクタンスは容量性インダクタンスと誘導性インダクタンスに分類される。
- レジスタンスは実数で、インダクタンスは虚数値で表される。
- レジスタンスは周波数に依存しないので、抵抗値をそのまま使用することができす。
- 容量性インダクタンスはキャパシタンス(コンデンサのC値)と周波数で表される。
- 誘導性インダクタンスはリアクタンス(コイルのL値)と周波数で表される。
- 交流回路も直流回路のように表すことができるが、実際には位相差が発生する場合があるので注意が必要。
になります。
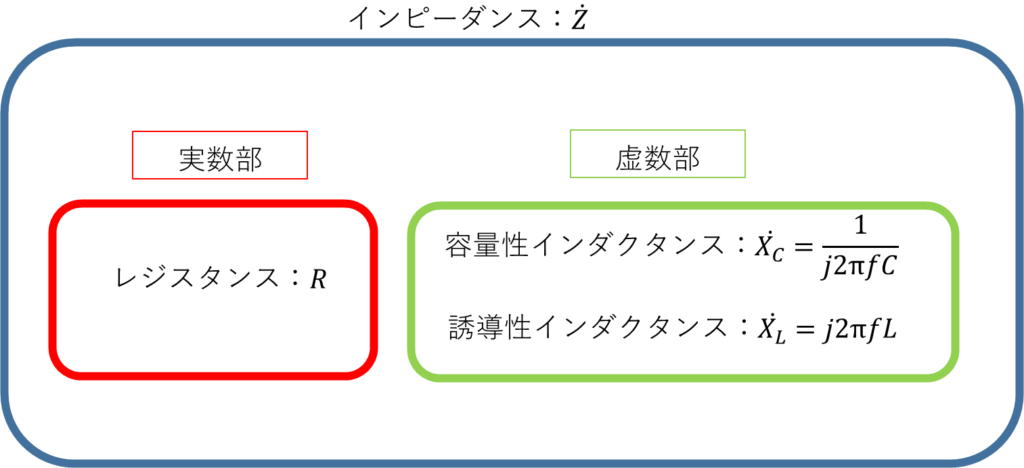
で、ようやく最初の話になりますが、抵抗(レジスタンス)はインピーダンスの中に含まれているので抵抗のことをインピーダンスと言っているのは問題ありません。
ただ、人によっては本来はコイルよコンデンサを含んでいるので、インピーダンスと言うべきところを「抵抗」言っている人はいました。(「だったらこの話は意味は無いがな!」と言われそうですが・・・)
雰囲気でインピーダンスと抵抗が混在して言ってくる人はいますので注意しましょう。(アイエルはそれを指摘したときメッチャ切れられたことがあります・・・)
最後に
交流回路は直流回路に比べて難しいです。先程述べましたが本来は微分方程式を理解する必要があります。しかし、すごい先人たちが交流理論を構築させることで微分方程式を理解できなくても交流を扱えるようにしてくれました。
なので交流理論で覚えた方が結果的に交流回路が計算できるようになり、そこから微分方程式を理解することでより交流を深く理解する逆説的なことになっています。
結論だけ覚えておくのは恥ずかしいことでは無くて有効な手段です。
例えば実行電圧の算出は√2で割りますが式から求めようとするとかなりメンドクサイので、結果だけ覚えてから余裕があれば式が導出できれば良いと思います。
このブログが皆さんの役に立てば幸いです。



