今回は抵抗並列回路計算についてです。
前回の直列回路編を見ていない場合は、先に見て頂ければと思います。
素子の接続は直列と並列の2種類ある
素子の接続方法は直列と並列にわけることができます。
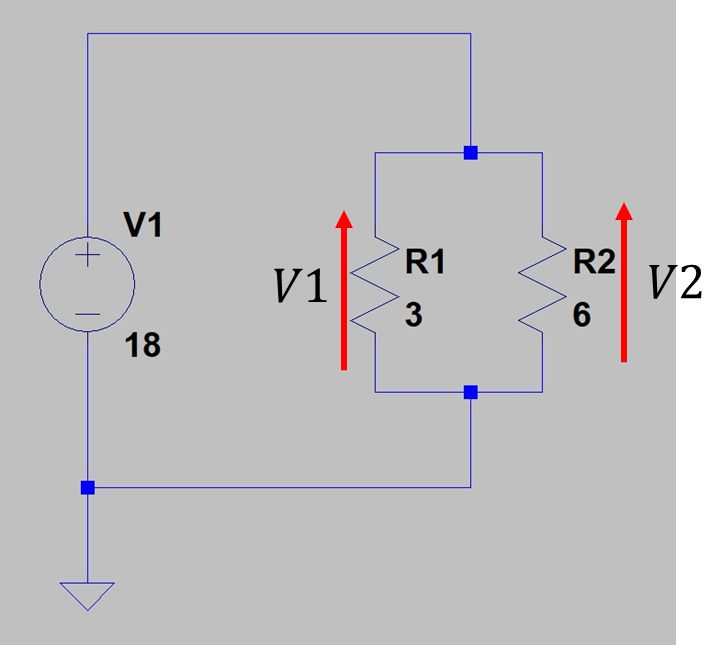
図1 抵抗並列回路
前回の抵抗を直列から並列に変えてみました。
これで各抵抗の電圧を計算すると・・・
うん、計算するまでもなく18Vになりますね。
そうなると電流も簡単に算出できます。(R1=6A、R2=3A)
では、次の場合はどうでしょうか。
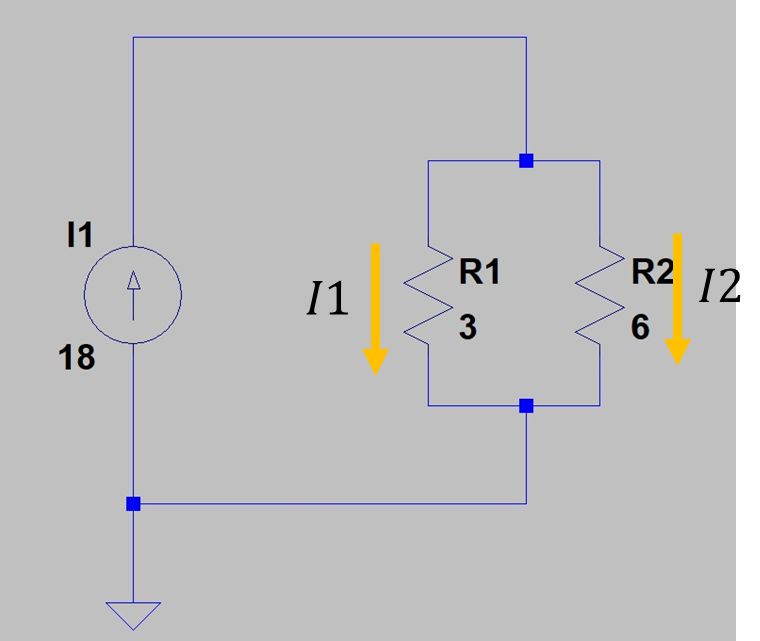
図2 抵抗並列回路2
図1から定電圧源18Vから定電流源18Aに変更しています。また求める物も抵抗の電流値にしています。
公式を知っている人は
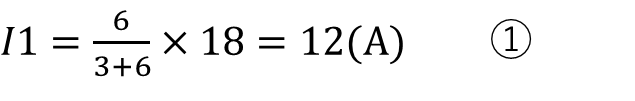
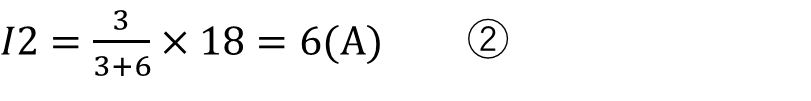
を算出できると思います。
しかし、抵抗直列回路回路と違い並列の3つの場合は少し混乱するかもしれません。
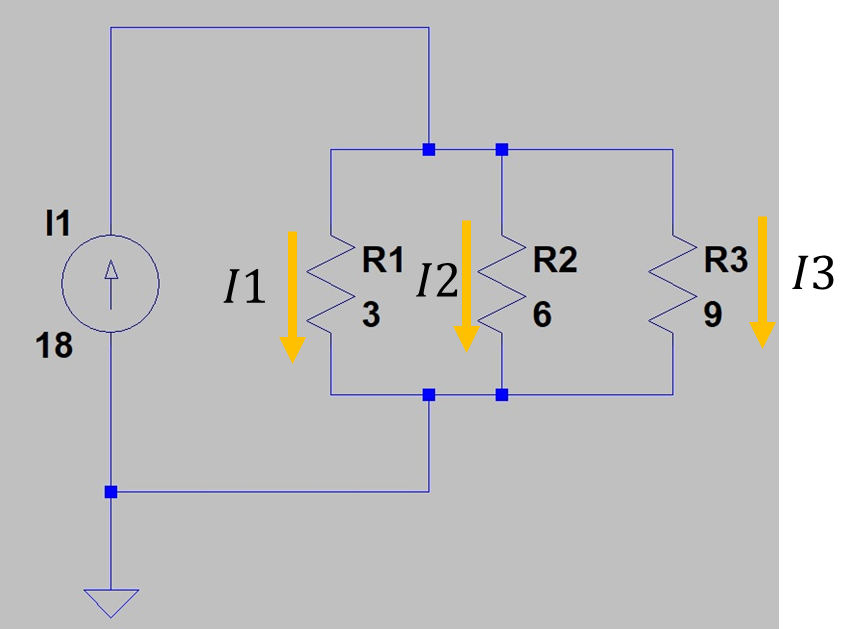
図3 抵抗並列回路3
抵抗素子2つだと難なく解けても3つになると「よくわからないな~」と思うかもしれません。今回はここの部分を解説したいと思います。
式の立て方は抵抗直列回路と同じ考え方
前回と同じように各素子と電源に電圧と電流を記入します。
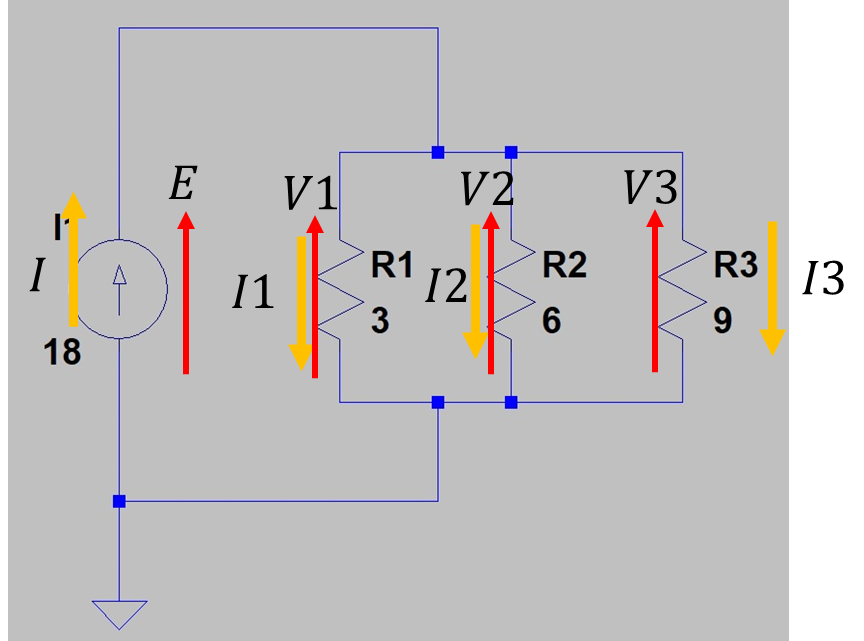
図4 抵抗並列回路4
見づらくてゴメンなさい・・・電圧は赤の矢印で電流はオレンジの矢印で表しています。
各素子と電源(定電圧源、定電流源に関係なく)に電圧と電流を振ることににより視覚的にわかりやすくなります。
前回同様にに電圧の高い方向よ電流の流れる方向を正側にしています。もし計算してマイナスになった場合は矢印が逆になることを意味します。(今回はそんな事はありませんが・・・)
まずはオームの法則より
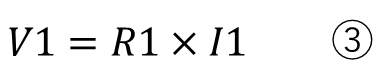
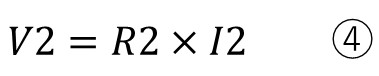
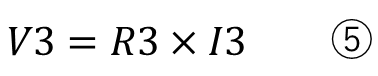
ここまでは同じです。
今回違うのは定電流源にしたことで、電源との関係は
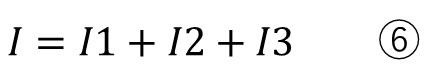
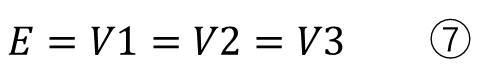
このようになります。ちょうど電圧と電流の関係が入れ替わっているような状態になります。
あとは前回と同じように計算するだけです。ただし、1つだけ気を付けて欲しいことがあります。
⑥に代入するために③~⑤の式を変形する必要があります。



これらを⑥に代入します
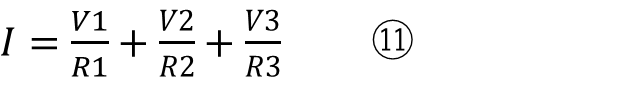
更に⑪に⑦を代入すると
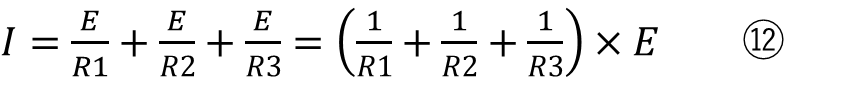
ここでI1を計算したい場合は⑫に⑦を入れれば良いので
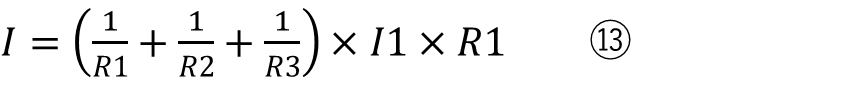
となりこれを整理すると
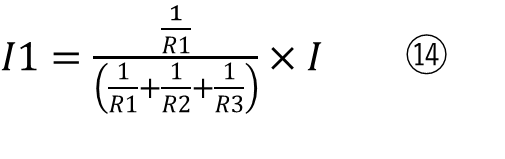
になります。
各抵抗値と全体の電流はわかっているので
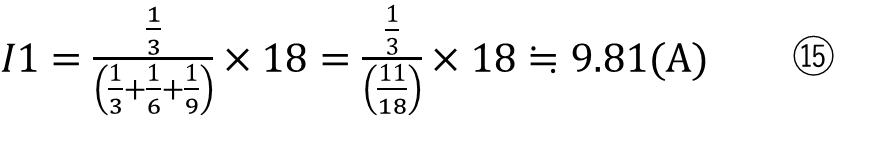
と計算することができます。
以上が抵抗並列回路の計算になります。
抵抗並列回路で一番重要なこと
抵抗並列回路の計算で一番重要なことはたった1つです。
それは・・・
各素子の電流は抵抗と反比例関係にあります。そして前提として各素子の電圧が同一だから先程の計算ができます。
全体の電流値がわかっていれば各素子の電流は抵抗の逆数で分配されます。(今回の場合は18Aは各素子に対して1/3:1/6:1/9の比率で流れている)
ここの部分がとても大事でこの前提が崩れるとこの方法では計算ができなくなります。
まとめ
今回のまとめです。
- 抵抗値に掛かる電流の総和と電源電流の値は等しい
- 抵抗直列回路は抵抗値と抵抗に掛かる電流は反比例関係である
- この計算ができるのは並列抵抗回路の各抵抗値の電圧が等しいからであり、直列だと各素子の電圧が同じにならないので成立しない
次回は直列並列回路について解説したいと思います。



