タイトルを見て「なんやこれ!」と思うかも知れませんがとても重要です。
電源って何?
突然ですが、電源って何だと思いますか?
アイエルのイメージは電池です。多くの人も電池のイメージが多いとは思いますが、回路設計の立場では接続した機器を動作させるために電気エネルギーを供給する機器となります。
電池は勿論、PCに接続するACアダプターや掃除機をつかうための壁側コンセントも電源になります。
電源は様々な種類もあり分類も色々あるのですが、今回は下記の様に2つに分けて説明します。
定電圧源
出力電圧を常に一定にする電源です。出力の負荷が可変しても電圧が変動しない(出力電流が負荷に合わせて可変する)回路が理想とされています。
イメージしやすいのは家電製品に使うコンセントで交流100V(以下AC100Vと記載)が発生していますが、電子レンジや掃除機等を使用してもこの100Vが維持されるようになっています。
広い意味では電池やコンデンサも電源として扱う場合もあります。
ただし、電池やコンデンサはエネルギーの充電状態で電圧に差があるので注意が必要です。
定電流源
出力電流を常に一定にする電源です。出力の負荷が可変しても電流がが変動しない(出力電圧が負荷に合わせて可変する)回路が理想とされています。
製品としては定電流ダイオード等がありますが使った事がある人は殆どいないと思います。
なので電源ってほとんどの場合は「定電圧源」を指します。
実際に回路設計は電圧を基準に組み立てていきます。
何故電源は定電圧源を指す場合がほとんどなのか?
計算では基本的に定電圧源、定電流源の両方で計算できないと単位や電気系の資格取得で困るかも知れませんが回路設計で定電流源を基準にすることはありません。
では、何故電源は定電圧源がメインになっているのでしょうか?
理由は以下の通りです。
1.発電所のは定電圧源で家庭に届けているから
日本の場合は一般的な家庭用の電圧はAC100V基準になっています。これに合致するように製品を設計しないとコンセントに接続すると動作不良が発生します。
ちなみに壁にあるコンセントに差し込む機器を発売するには、コンセントに差し込んでも問題無い製品であることを証明するPSEマークを取得する必要があります。
2.半導体の定格に電圧が定められているから
大昔の機器はAC100Vで直接制御していました。扇風機や冷蔵庫を始めとした家電は全てメカニカルなスイッチで制御しており、リモコンなんかありませんでした。整流や制御は真空管の時代でした。
しかし、トランジスタが実用化されて小型で軽量な製品ができるようになりました。このトランジスタが進化してICやマイコンチップになるのですが、アイエルが仕事で関わるときは5Vか3.3Vで動作するICが殆どでした。最近でこそパワエレ系の高圧の半導体が台頭してきましたが、汎用のトランジスタは概ね30V以上の電圧で破壊されます。
3.電池が直流定電圧源だから
携帯性のある電子機器は電池で動作します。またPCやスマホの電池に充電するACアダプターは出力は直流定電圧源です。充放電できる電池は直流で動作する半導体との相性がよいのです。
他の分け方では交流(AC)、直流(DC)等ありますが、交流の計算は直流の計算が理解できていないと厳しいので今回は基本の定電圧源と定電流源で解説していきたいと思います。
でようやく電源と直列並列接続抵抗との関係に入ります
回路の計算問題で抵抗値がわかっている場合では2種類に分類されます。
- 抵抗が直列接続で抵抗値と定電圧源の電圧が既知で1つの抵抗に掛かる電圧を算出する
- 抵抗が並列接続で抵抗値と定電流源の電流が既知で1つの抵抗に掛かる電流を算出する
解き方については過去の投稿を参照ください。要約すると
- 抵抗が直列接続で抵抗値と定電圧源の電圧が既知で1つの抵抗に掛かる電圧を算出する(定電圧源と抵抗の電流値が同じになっているのを利用する)
- 抵抗が並列接続で抵抗値と定電流源の電流が既知で1つの抵抗に掛かる電流を算出する(定電流源と抵抗の電圧値が同じになっているのを利用する)
になります。
逆のパターンは
- 抵抗が並列接続で抵抗値と定電圧源の電圧が既知で1つの抵抗に掛かる電流を算出する
- 抵抗が直列接続で抵抗値と定電流源の電流が既知で1つの抵抗に掛かる電圧を算出する
になりますが、それぞれの抵抗でオームの法則に必要な値がわかっていますので解説する価値はありません。
計算の方法は電源の種類、抵抗の接続方法と問わずどれでも下記の3ステップで解くことができます。
- 電源と各抵抗に電圧ベクトルを電流ベクトルを記入する
- 各抵抗のオームの法則を記載する
- 電源と抵抗の電圧の関係式と電流の関係式を作成する
- ②と③で出した連立方程式を解く
これがめちゃくちゃ重要で回路試験の問題はこれがわかれば。
具体的には
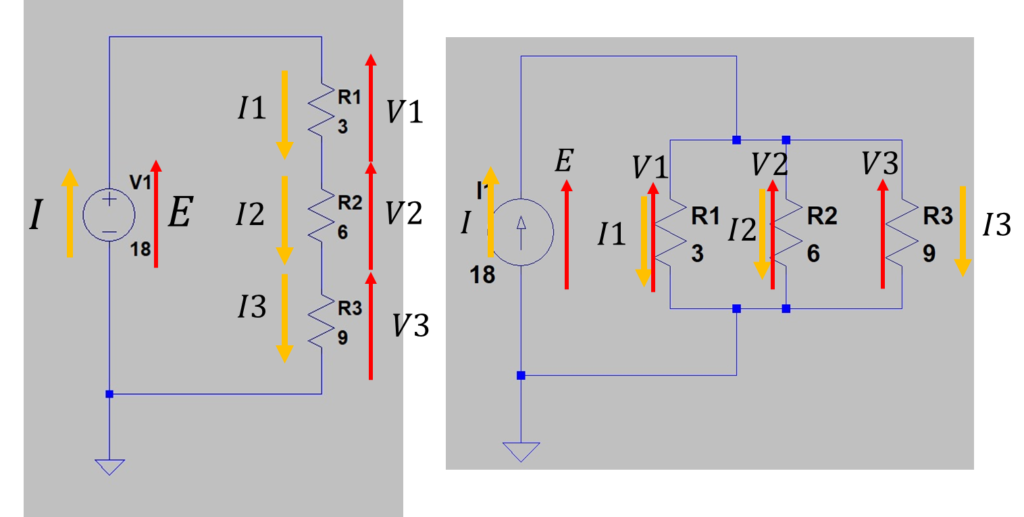
図1 直列回路(左)並列回路(右)
図1は①電源と各抵抗に電圧ベクトルを電流ベクトルを記載する部分になります。
回路に関係なく抵抗に掛かる電圧と電流は
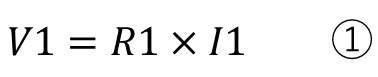
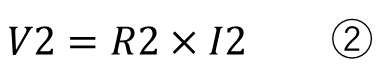
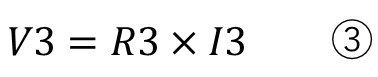
になります。この部分は直列回路でも並列回路回路でも変わりません。
違うのは電源との関係です。
直列回路では電源の電流と各抵抗に流れる電流は同じで、電源の電圧と各抵抗の和が同じになります。
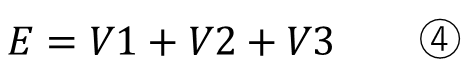
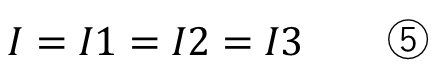
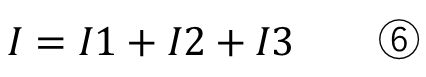
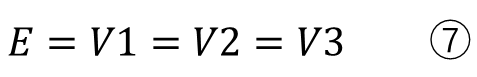
ここさえ理解できれば後は数学的に連立方程式を解くだけです。
そしてようやく直並列の計算へ
でここで直並列回路を解いてみましょう。
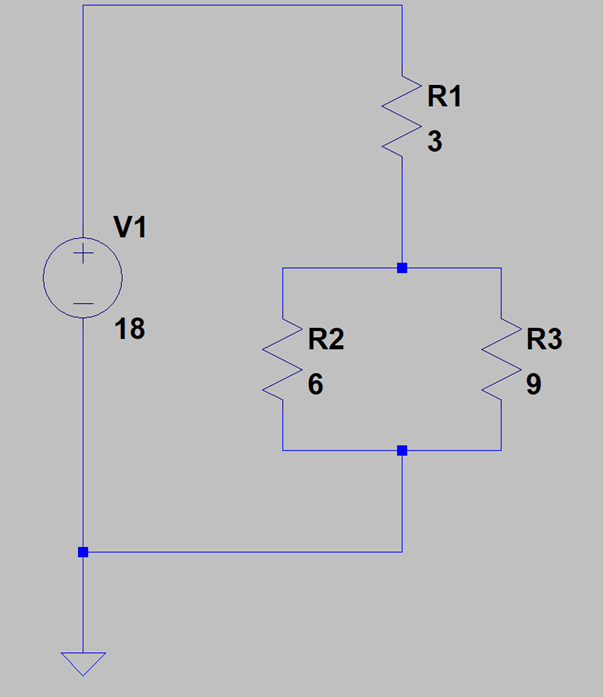
図2 直並列接続回路
やり方はこれまでと同じで、電源と抵抗に電圧ベクトルと電流ベクトルを記入します。
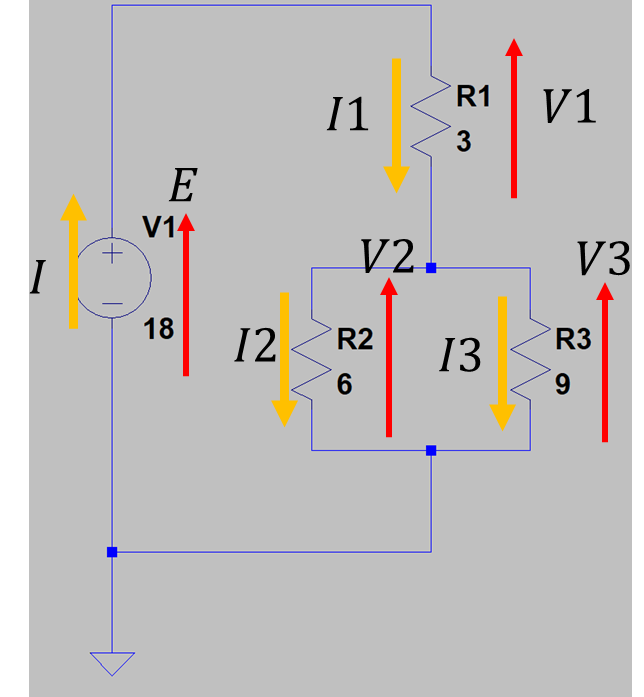
図3 図2に電圧、電流ベクトル記入
つぎに各抵抗のオームの法則を記載します。
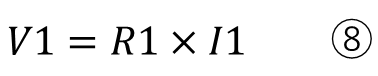
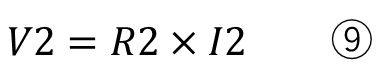
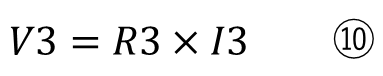
ここまでは今までと全くおなじです。ここから注意して欲しいのが、
電源の電圧及び電流と抵抗の電圧と電流の関係性は回路によって変わります。
今回の回路の場合は
- 電圧はR2とR3が並列接続になっているので電圧は同じことに注意して抵抗直列回路のように計算する。
- 電流は電源電流とI1が同じことに注意して、抵抗並列回路のように計算する。
ベクトルを入れたことで視覚的にわかりやすくっていると思います。
整理すると
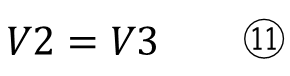
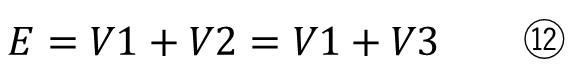
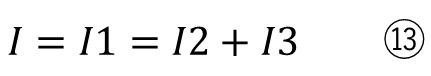
になります。
V1を求めるためにはI1を求める必要があります。しかしR2とR3は並列に接続しているため各抵抗に流れている電流はおなじではありません。
わかっているのは電源電圧と各抵抗値ですのでうまいこと電流Iを消して行く必要があります。
⑫に①~③を代入すると
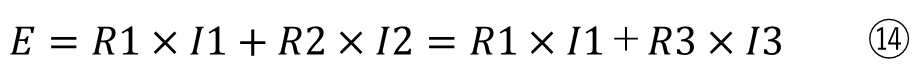
整理すると
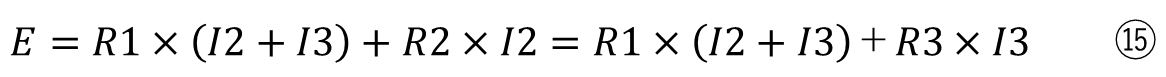
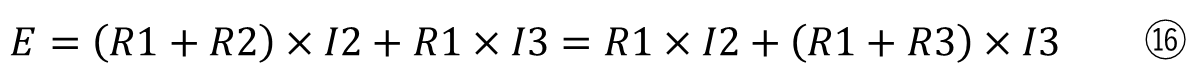
この⑯は2つの式が結合しているので、2つに分けると
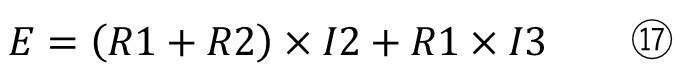
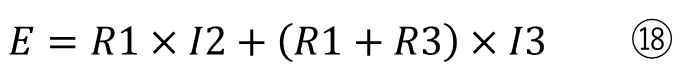
になり、この連立方程式を解くとI2とI3を求めることができます。
実際に代入してみると
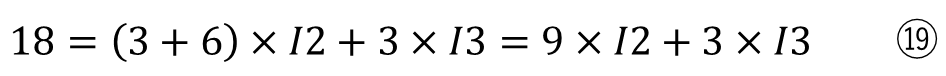
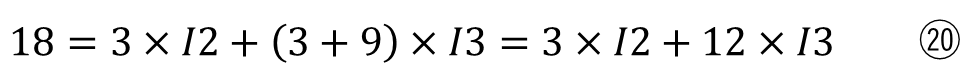
になり⑲と⑳の連立方程式を解くと
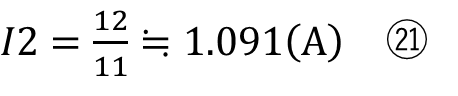
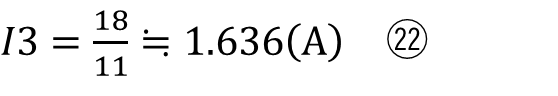
が算出できます。これらを⑬に代入すると
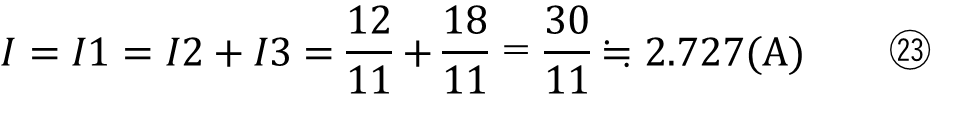
これを⑧に代入すると
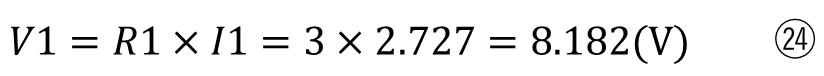
でV1を求めることができます。
ちなみに、R2とR3も同様にして㉑及び㉒で算出した値を②と③に代入して求めると電圧は9.818Vと算出できます。この値とV1を足すと18Vになります。
検算をしてしっかりと確認することは重要です。
まとめ
今回は抵抗の直列と並列混在した回路について解説しました。作業的な手順は以下になります。
- 抵抗が直列と並列が混在している場合も計算することはできる
- 抵抗直列回路と抵抗並列回路を理解している必要がある
- 電源の電圧値と各素子の電圧の関係式を立てる
- 電源の電流値と各素子の電流の関係式を立てる
- 1次の連立方程式を解く
- 検算を行う
回路素子数が多くなると計算がややこしくなると思いますが、1次の連立方程式なので高校数学で対応できる範囲です。
電源と素子の関係式を作成するにはある程度の経験が必要ですが、慣れれば簡単にできるようになります。
アイエルも式の立て方は始めは苦労しましたが慣れれば問題ないです。むしろ計算間違いが多くて検算で合わないときに自己嫌悪に陥ることが多かったです。
これらが解けるようになると、電気回路の計算に重要な「キルヒホッフの法則」が理解できるようになると思います。
電気回路を勉強する場合は、抵抗だけではなく色々な素子を学んで計算するようになります。ですが、
どんな素子も接続方法は直列か並列しか存在しない!
これさえ覚えていれば、直列や並列に分割して計算すれば良いだけと思えるようになります。(アイエルの経験になりますが)
長々と説明しましたが、これらが皆様の役に立てば良いなと思います。


